Testing concurrent programs is hard, because there are many valid schedules: but only one will be used by a given execution. This means we can’t just run something once to be confident it’s right.
- How many times do we need to run it?
- Does the number of runs we need grow with relation to the program?
- Is this even a good approach?
Running the program lots of times might be ok if every run uses a unique schedule, otherwise you’ll explore less of the possibility space than you might think. Even if you can guarantee uniqueness of schedules, larger programs tend to have more possible schedules, so you need more runs to get the same coverage guarantee: but it’s difficult to know exactly how many.
So random testing is out. Let’s see what the alternatives are.
Schedule Bounding
Completeness in concurrency testing is hard, we’d already given up on it when we considered random testing, so why not throw it out in a much more principled fashion?
Enter schedule bounding. Here, we define some bound function which, given a list of scheduling decisions, will determine if that is within the bound or not. We then test all schedules within the bound.
There are a few bound functions in common use:
- Pre-emption bounding: restricting the number of pre-emptive context switches.
- Delay bounding: restricting the number of deviations from an otherwise deterministic scheduler.
- Fair bounding: restricting the number of consecutive times a non-blocking loop accessing shared state (like a spinlock) is executed.
Furthermore, these bound functions are often iterated. For example, trying all schedules with 0 pre-emptions, then trying all schedules with 1 pre-emption, and so on, up to some limit.
Pre-emption bounding is a common one, and empirical studies1 have found that test cases with as few as two threads and two pre-emptions are enough to find many concurrency bugs.
Diversion: Generating Schedules
You may be wondering how schedule bounding can actually be implemented. Maybe you’re wondering if you simply monitor the execution and abort it if it exceeds the bound.
Well, that would certainly enforce the bound, but it wouldn’t give you many coverage guarantees in finite time.
By executing a program you can gather a lot of information: things like, what threads are runnable at each step (and what they would do if you scheduled them), what the thread that was scheduled did, the state of all shared variables (for CVars/MVars, this is whether they’re full or empty). You can use this to inform your initial set of scheduling decisions when starting a new execution, to systematically explore the possibility space.
You can store this information in a tree structure modified between executions: each edge represents a scheduling decision, each node contains information on the threads runnable at that point, and the alternative decisions still to make. This turns out to be quite a space-efficient representation, as schedule prefixes are explicitly shared as much as possible.
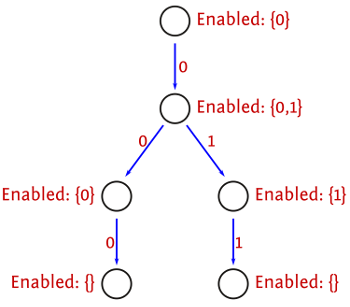
Blocking Avoidance
If we have a bunch of runnable threads, but some of them will block immediately without modifying any shared state, then we can restrict the set of runnable threads to those which won’t block.
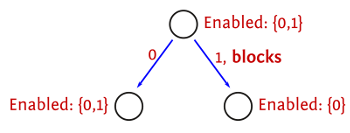
This is safe when there’s no schedule bounding happening, or when it can’t result in otherwise legal schedules no longer being legal.
In the case of pre-emption bounding, this is safe because it doesn’t alter the pre-emption count of any schedules reachable from this state, as if a thread blocks then any other thread can be executed without incurring an extra pre-emption.
Partial-order Reduction
Eliminating schedules which obviously don’t change the state is a nice step, but it’s only a first step.
We can characterise the execution of a concurrent program by the ordering of dependent actions, such as reads and writes to the same variable. This is a partial order on the program actions, for which there may be many total orders. Ideally, we would only check one total order for each partial order, as different total orders will have the same result.
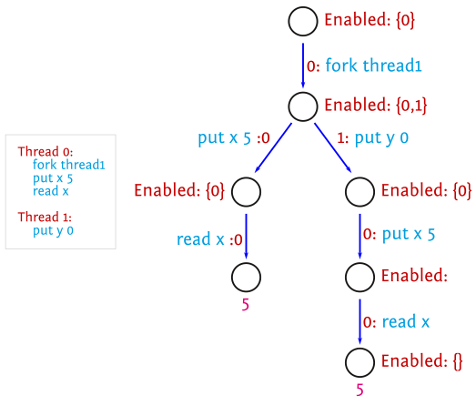
Partial-order reduction (POR) can be implemented by only exploring multiple scheduling decisions (when there is a choice) if they can interfere with each other.
Unfortunately, POR isn’t quite that simple when using schedule bounding, as it can impose dependencies between previously-unrelated actions, as they can affect whether a state is reachable within the bound or not.
How this is solved depends on the specific bound function used. For pre-emption bounding, it suffices to try different possibilities when a context switch happens. Furthermore, when implementing blocking avoidance, don’t remove the context switch entirely, instead perform it earlier in the execution, where it won’t block.
Sleep Sets
Unfortunately, the context switches introduced by POR can still result in the same program state being reached by multiple different schedules.
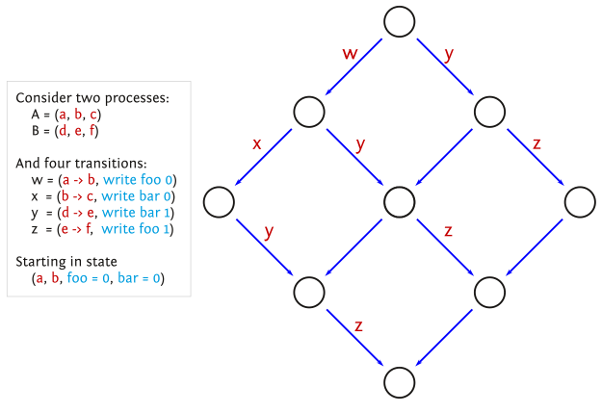
Sleep sets are a complementary improvement, which do not require POR. The idea is that, if you have two or more decisions to make, and you have explored one possibility, there’s no point in making that same decision when trying the other possibility, unless something happens which can alter the result. If nothing has changed, you’ll get the same result.
The Déjà Fu Approach
Déjà Fu uses a combination of all of these approaches, including some tweaks to the order of schedule exploration to try to find bugs sooner rather than later, when there are any.
The algorithm used by the standard testing functions is pre-emption bounded partial-order reduction, with a bound of 2, using blocking avoidance (note that that doesn’t reduce the number of schedules when used in conjuction with bounded partial-order reduction!) and sleep sets. Enough of the internals are exposed to allow implementing your own bound function, such as fairness bounding or delay bounding.
To give some figures, here’s the effect of every improvement to the algorithm for runPar $ parMap id [1..5] with the Par monad’s “direct” scheduler:
- Pre-emption bounding: 12539 unique schedules,
- + blocking avoidance: 11400,
- + partial-order reduction: 8181,
- + sleep sets: 2237.
As can be seen, sleep sets are a massive improvement in this case, and I would wager that just pre-emption bounding with sleep sets would also see a similar improvement. Obviously this is a very simple example, with little communication between threads, and so can’t really be generalised to other cases, but it’s a nice result.
P. Thomson, A. F. Donaldson, and A. Betts. Concurrency Testing Using Schedule Bounding: an Empirical Study. In Proceedings of the 19th ACM SIGPLAN symposium on Principles and Practice of Parallel Programming, pages 15–28. ACM, 2014.↩︎